CRを使用した微分回路の紹介です。
回路は単純ですが考えてみると意外に奥が深いです。
用途としてはパルス検出等に使用される事があると思います。
微分回路の回路構成
CR方式の微分回路は以下となります。
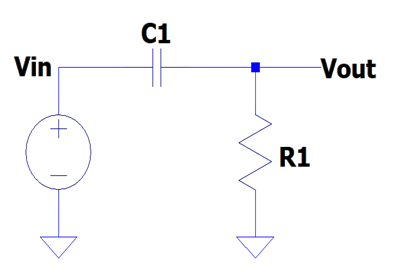
微分回路の由来は
入力電圧(Vin)の電圧変化を時間で微分した波形を出力電圧(Vout)として出すことが由来。簡単に言うと入力電圧が変化した時に出力電圧が発生。
微分回路の動作
微分回路に矩形波を入力した場合の出力波形は以下となります。
但し、条件がありt1に対してCRの掛け算である時定数に対し十分小さい場合です。
※別途、詳しく説明
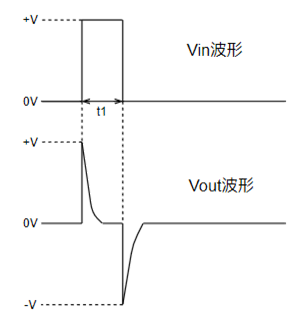
入力電圧(Vin)が0⇒5Vに変化した時(t=0、Vout=0の場合)
①C1に充電されている電圧は0Vとなる。
②Vinの全電圧はR1に入力されるためVout=Vinの電圧となる。
(C1がショートしているとみなせる)
③Voutの電圧がVinになると徐々にC1に電圧が充電される。
④Voutの電圧は徐々に減衰して最終的には0Vとなる。
入力電圧(Vin)が5V⇒0に変化したとき
①C1に充電されている電圧は5Vとなる。
②Vinが0Vになると-5Vの電圧がVoutに表れる。
③Voutの電圧が-5Vになると徐々に放電されてVoutは0Vとなる。
出力電圧の計算式
入力電圧が0⇒5Vに変化した時
$$Vout=Vine^\frac{-t}{CR}$$
上記式よりt=0の時、exp(0)=1となるためVout=Vinとなります。
入力電圧が5V⇒0に変化した時
$$Vout=Vine^{-\frac{t-T}{CR}}$$
設計する上でのポイント
以下2点のポイントを紹介します。
設計する際は必ず考慮する必要があります。
時定数はt1に対して十分小さい値とする
t1に対してCRの時定数が大きいと微分回路としては働かないため注意が必要です。
目安としてはt1に対して時定数は1/10以下にする必要があります。
以下に例を示します。
・条件:t1=0.1msの場合
①時定数=0.1ms(時定数=t1)の場合
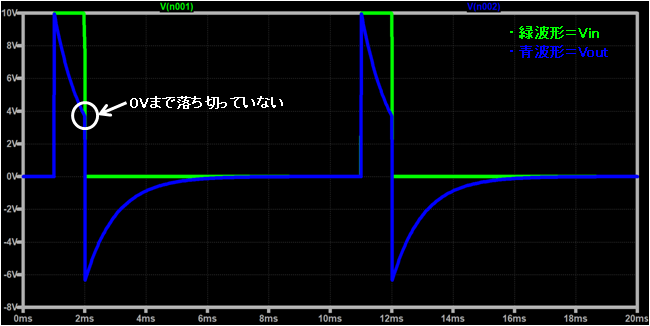
②時定数=0.05ms(時定数=1/2*t1)の場合
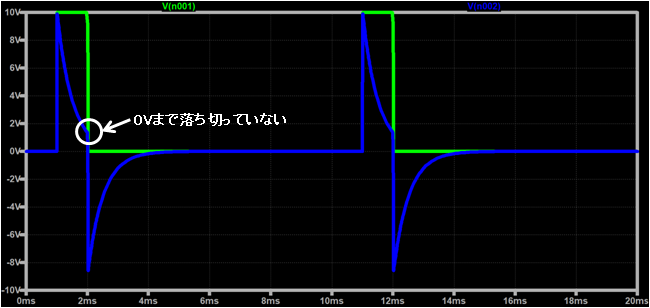
③時定数=0.025ms(時定数=1/4*t1)の場合
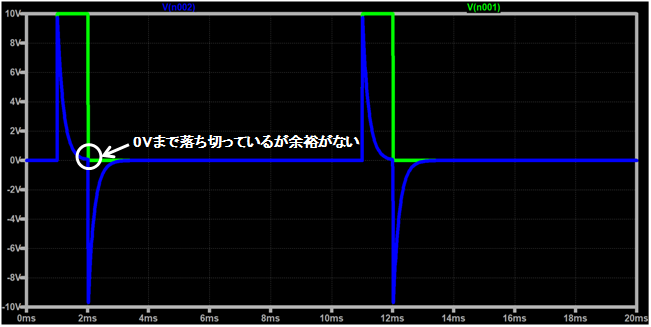
④時定数=0.02ms(時定数=1/5*t1)の場合
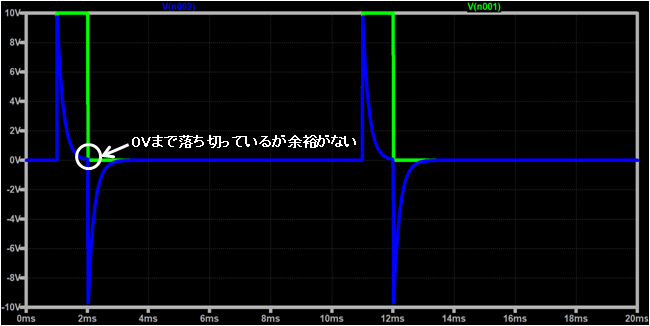
⑤時定数=0.01ms(時定数=1/10*t1)の場合
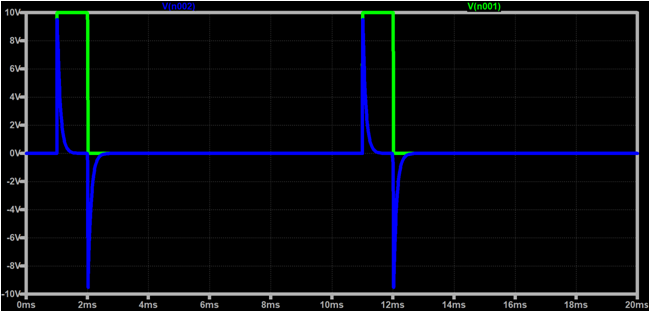
時定数の抵抗値は回路の出力電流を満足する値とする
微分回路の時定数はCとRの掛け算となります。
時定数が1msの場合
・抵抗値=1kΩ、コンデンサ=1uF
・抵抗値=10kΩ、コンデンサ=0.1uF
はどちらも時定数は1msとなりますが実際に回路に流れる電流は異なります。
理由として微分回路の電流は以下式となります。
入力電圧が0⇒5Vに変化した時
$$Iout={\frac{Vin}{R}}e^{-\frac{t}{CR}}$$
上記よりVinとRで割った値が出力電流として流れます。
時定数はCの容量とRの抵抗値を掛けた値のためCの容量を大きくすれば時定数を大きくすることができます。ただ、あまり容量を大きくすることで時定数を大きくした結果、抵抗値が小さい値となると出力電流として流れる電流が増えます。
よって、定数を検討する際は微分回路を接続する入力回路が供給できる電流値を確認した上で抵抗値の定数を検討する必要があります。



コメント