RC方式の積分回路の動作と設計ポイントを詳しく紹介！

紹介するのは抵抗とコンデンサを使用した積分回路です。回路構成からローパスフィルタとして使用する際の考え方をシュミレーション波形を交えながら説明するようにしています。

RC方式の積分回路の構成

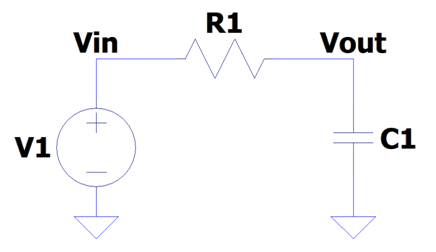
回路構成は以下となります。抵抗とコンデンサを使用した非常にシンプルな回路で微分回路に対して抵抗とコンデンサを逆にした回路です。

RC方式の積分回路に電圧がE[V]の矩形波を入力した場合の波形は以下となります。入力のVinに対して出力のVoutは遅れて電圧が上昇し最終的にはVinと同じE[V]になります。

出力電圧のVoutの電圧は以下計算式で算出できます。

$$Vout=E(1-e^\frac{-t}{CR})$$

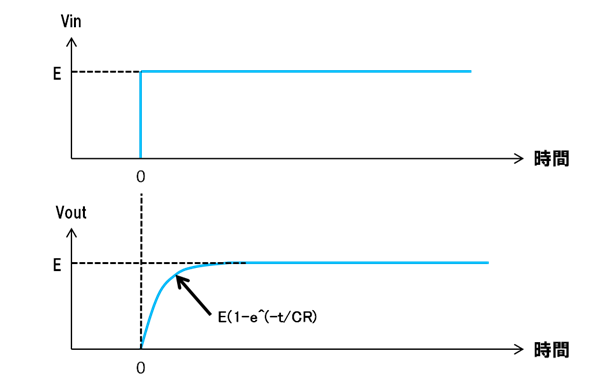
この部分で最低限知っておく必要があることは以下の4点です。

RC方式の積分回路の周波数特性について紹介します。冒頭でも述べたようにローパスフィルタとして働きます。ローパスフィルタとは低周波の信号は通して高周波の信号は通さない、言い換えれば、高周波ノイズを除去する回路として働きます。

より詳しく説明するため以下回路を組んでシュミレーションを行いました。R1の抵抗は10kΩ、C1のコンデンサは0.01uとなっているため時定数は100usとなります。

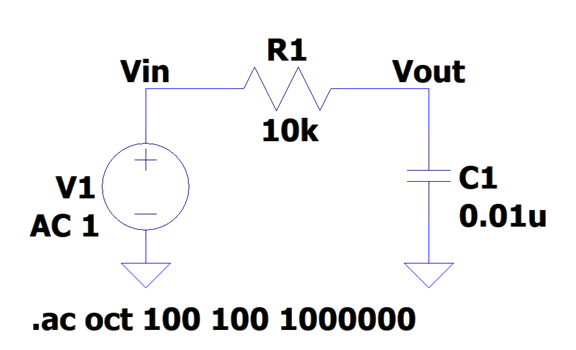
普通の線で示されているのが『ゲイン』で単位はdBとなります。『ゲイン』とは入力電圧に対する出力電圧の比率と考えると分かりやすいと思います。『ゲイン』は以下式で算出できます。

$$ゲイン=\frac{1}{\sqrt{1+(ωCR)^2}}$$

点線で示されているのが『位相』で単位は°になります。『位相』とは入力電圧の位相に対する出力電圧の位相の差（変化量)となります。『位相』は以下式で算出できます。

$$位相＝-tan^{-1}(ωCR)$$

RC積分回路で重要な言葉としてカットオフ周波数があります。

基本的な設計手順は以下となります。

設計する上でのポイントは以下となります

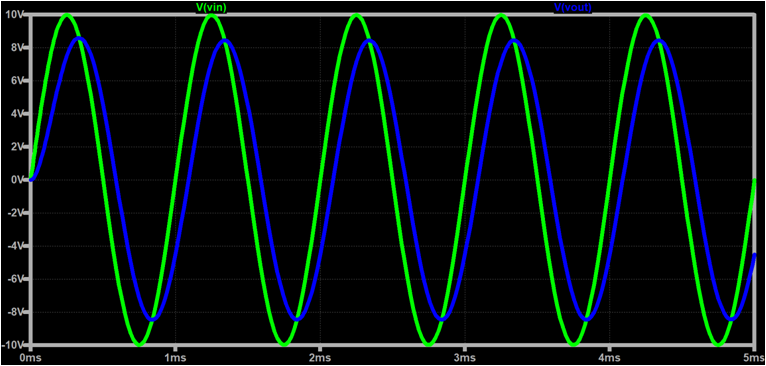
注意点としてはカットオフ周波数でも出力電圧は入力電圧に対し1/√2倍となり位相も約45°ズレます。そのため入力信号をそのまま通過させたい場合はカットオフ周波数は入力信号の周波数に対して10倍程度高くする必要があります。

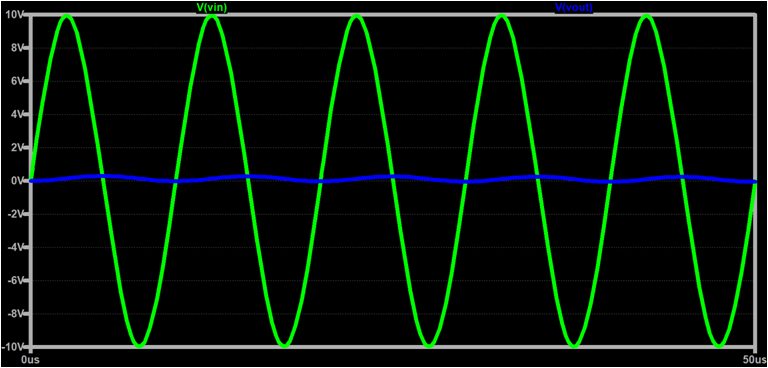
最後に参考としてシュミレーション波形で上記内容を確認します。